Dimitra Maoutsa 






[work in progress...] We are developing a framework for identifying latent stochastic dynamics from spike train observations. We reformulate the inference in terms of stochastic control and employ the deterministic particle control framework to sample the unobserved path distribution.
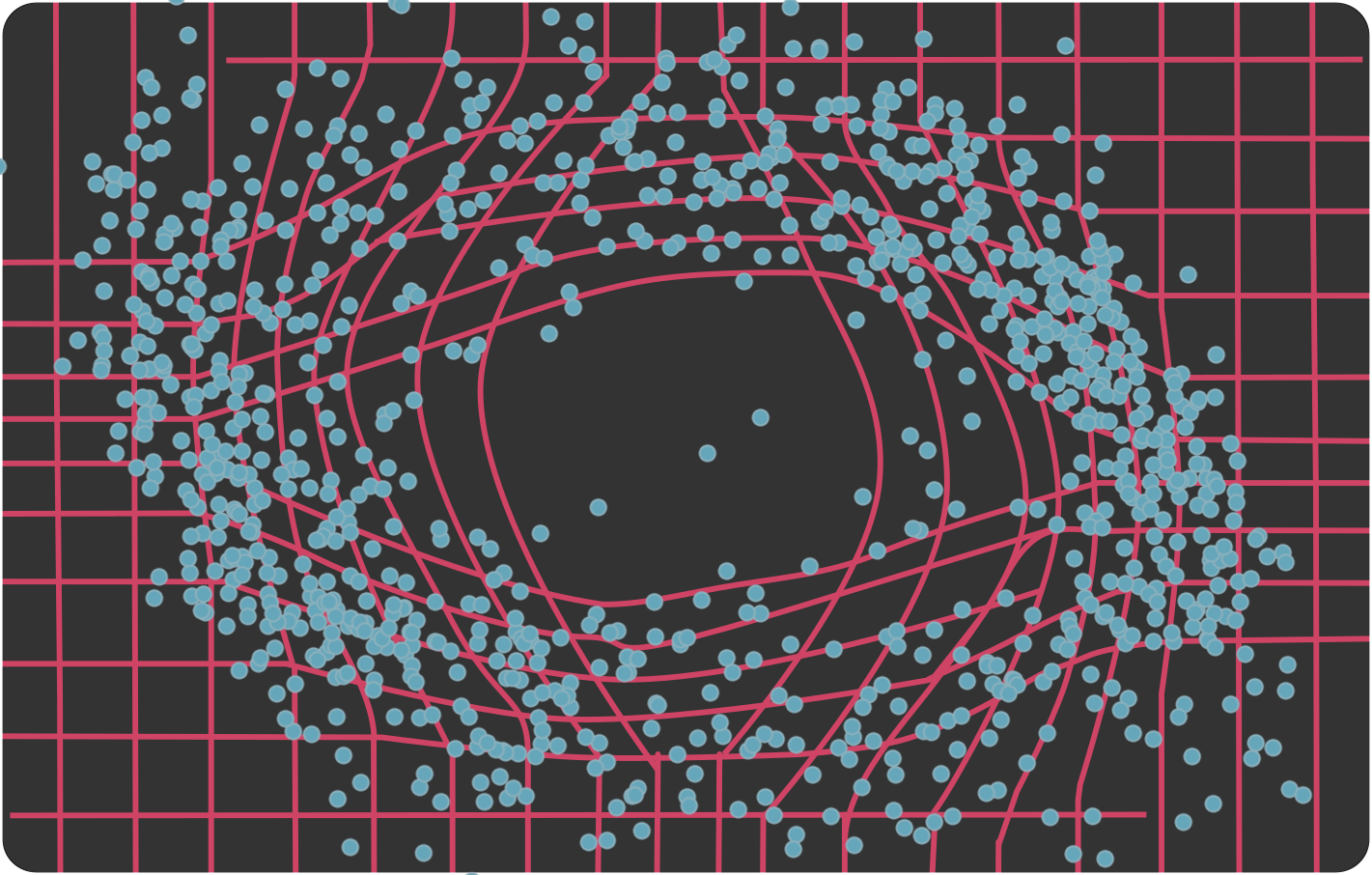
Reconciling geometric and path-space approaches for identifying diffusion processes.
We employed insights from nonlinear dynamics, Riemannian geometry, and stochastic analysis to device a novel path augmentation framework that allows for efficient and accurate inference of stochastic nonlinear systems.
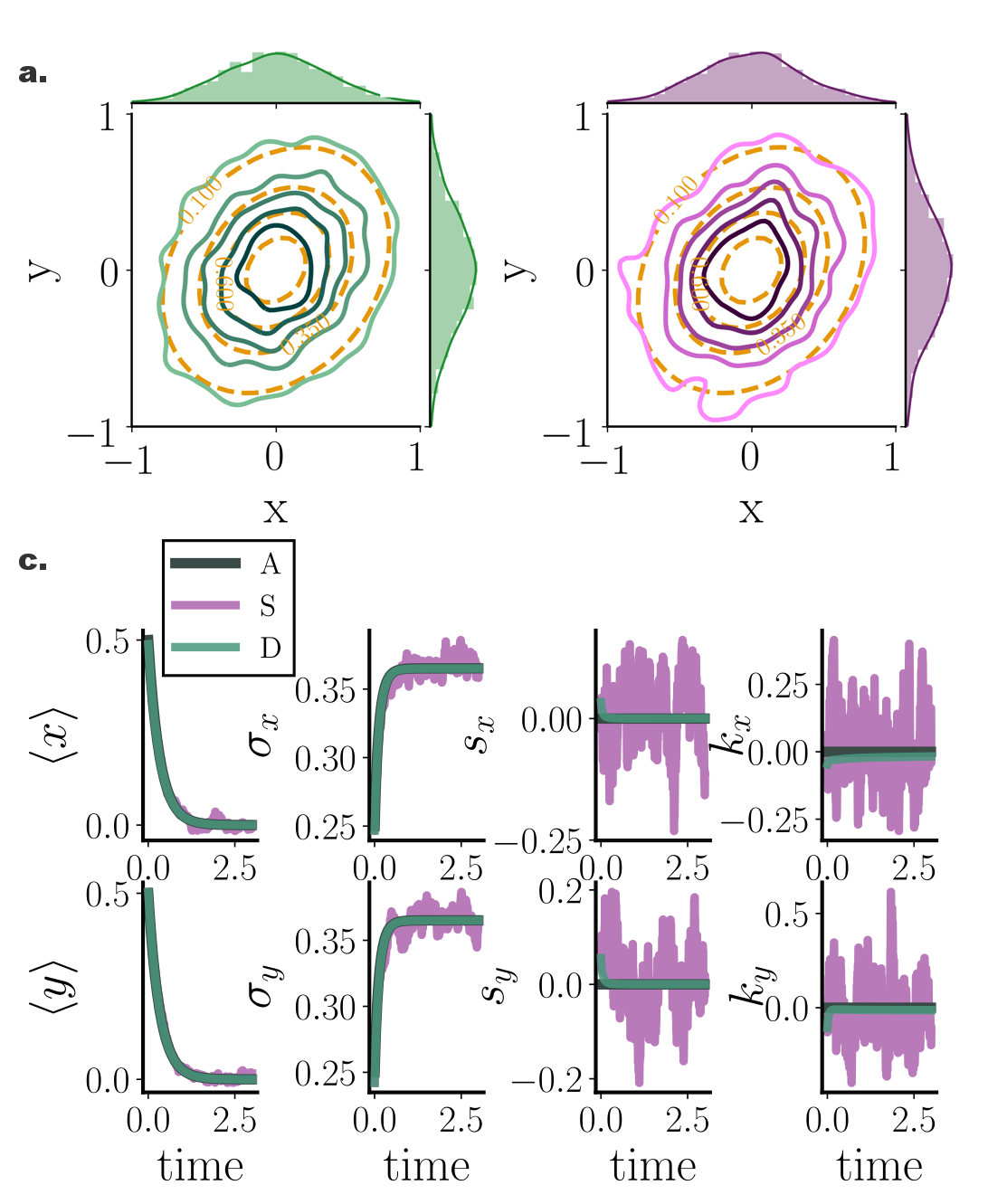
A computational method for fast and efficient simulation of transient Fokker--Planck equation solutions.
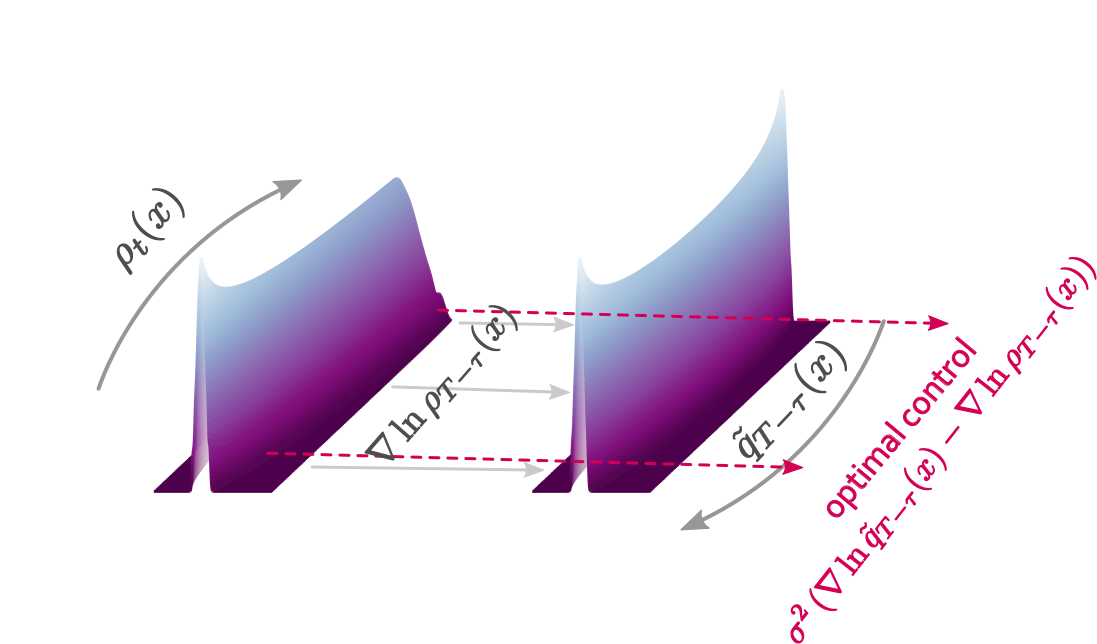
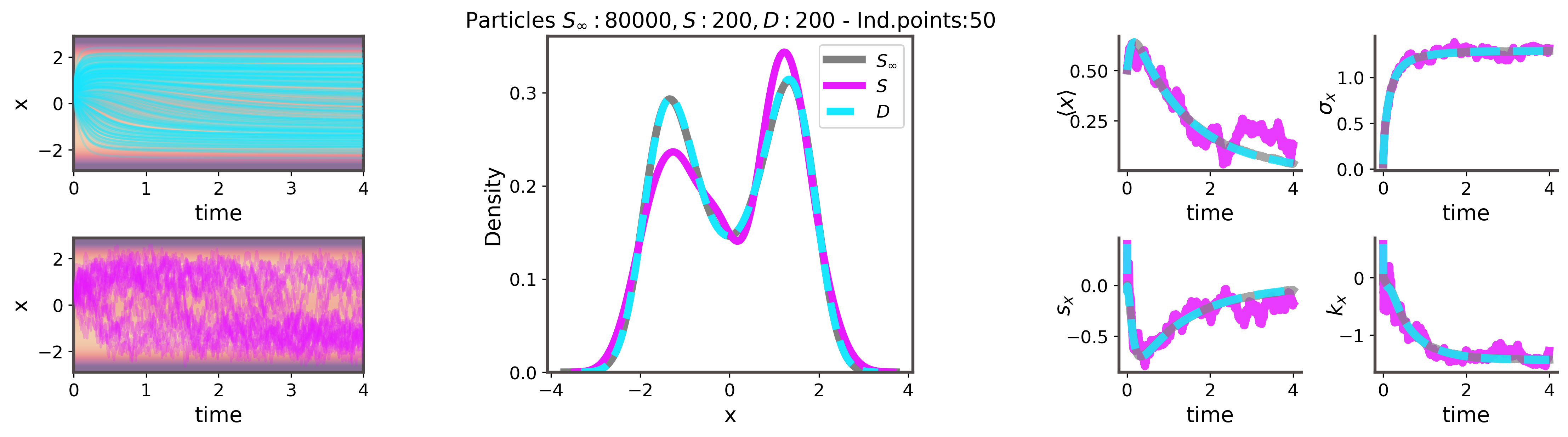
We introduced an interacting particle system with purely deterministic dynamics that provides accurate Fokker--Planck solutions for diffusive systems. The formulation relies on a variational representation of the logarithmic gradient of the instaneous Fokker-Planck probability density. Our approach does not require the knowledge (or even the existence) of a steady state, and is thereby relevant even for systems with time inhomogeneous dynamics.
Inferring synaptic interactions and transmission delays
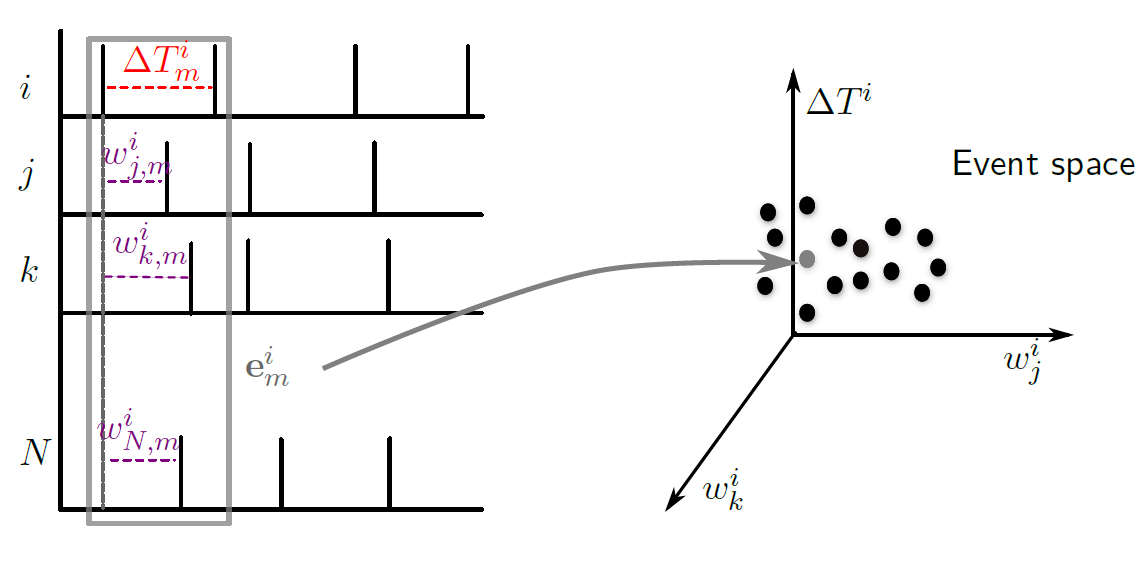
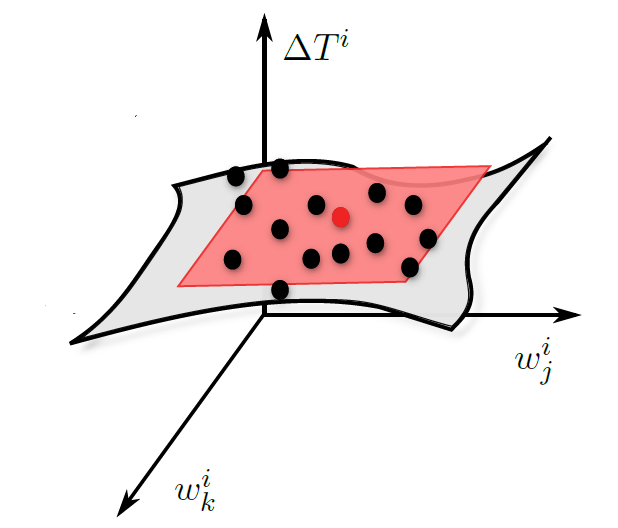
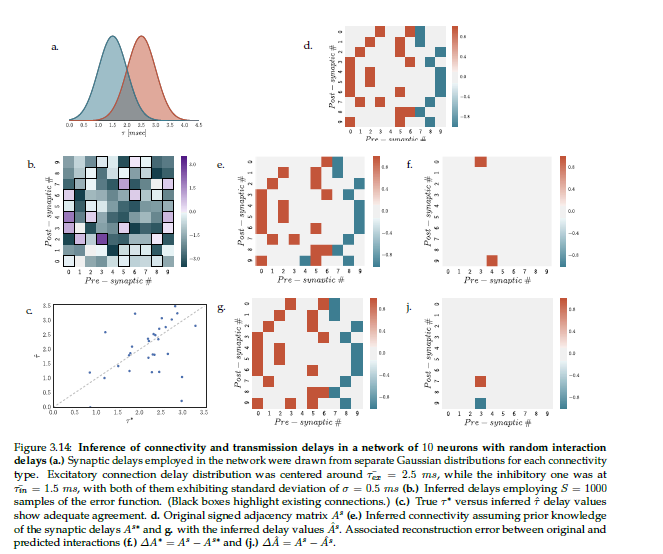
Inference method for identifying synaptic interactions and transmission delays from spiking activity.
We proposed a mapping of the spiking activity to high-dimensional spaces, called event spaces, spanned by the inter-spike intervals of a selected neuron and the respective cross-spike intervals of the rest of the network. The mapping from the raster plot to the event spaces may be viewed as a sampling of the inter-spike interval generating function for each neuron. To identify the effect of putative pre-synaptic neurons to a post-synaptic one we proposed a linearisation of the inter-spike interval generating function around a reference point (reference event).
To identify the transmission delays, we proposed the minimisation of the approximation error in the space of interaction delays. To speed up the optimisation and avoid local minima, we optimised the delays on a smoothed error landscape approximated by radial basis function interpolation.
Perturbing spiking neural networks with structured connectivity
Can one hear the shape of a network?
Small project on spreading perturbations on spiking neural networks. I found that the relaxation of the network activity to an attracting collective reference state may reveal global properties of the underlying network structure in terms of the first few eigenvectors of the connectivity matrix.