Identifying stochastic systems from discrete time observations

Sisyphus

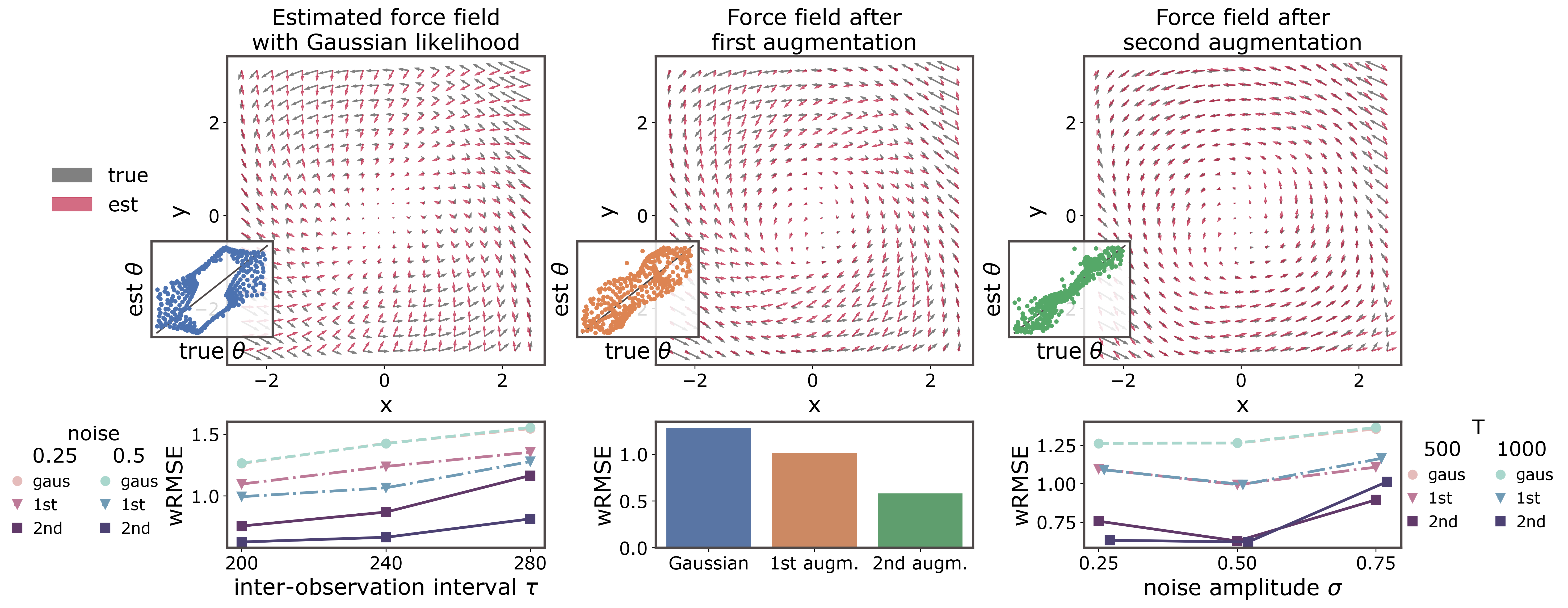
Estimation of sparsely observed diffusions with Gaussian likelihood assumptions results in inaccurately estimated force fields.

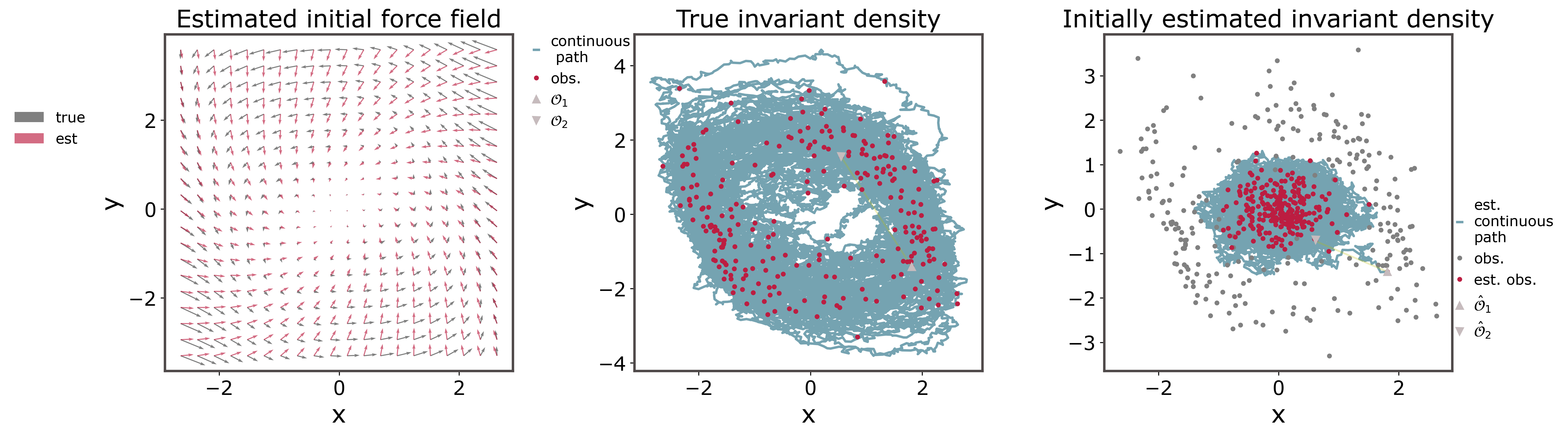
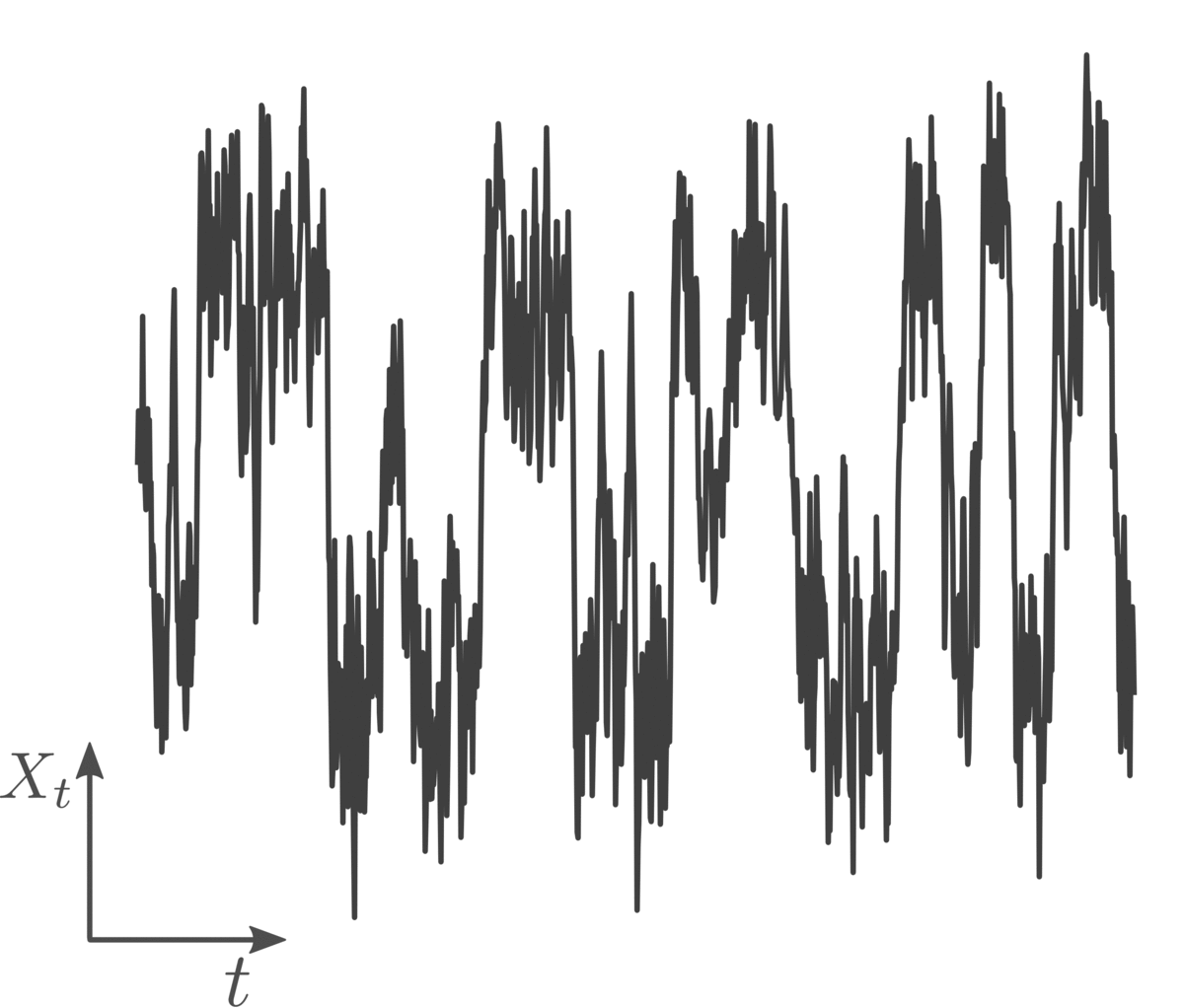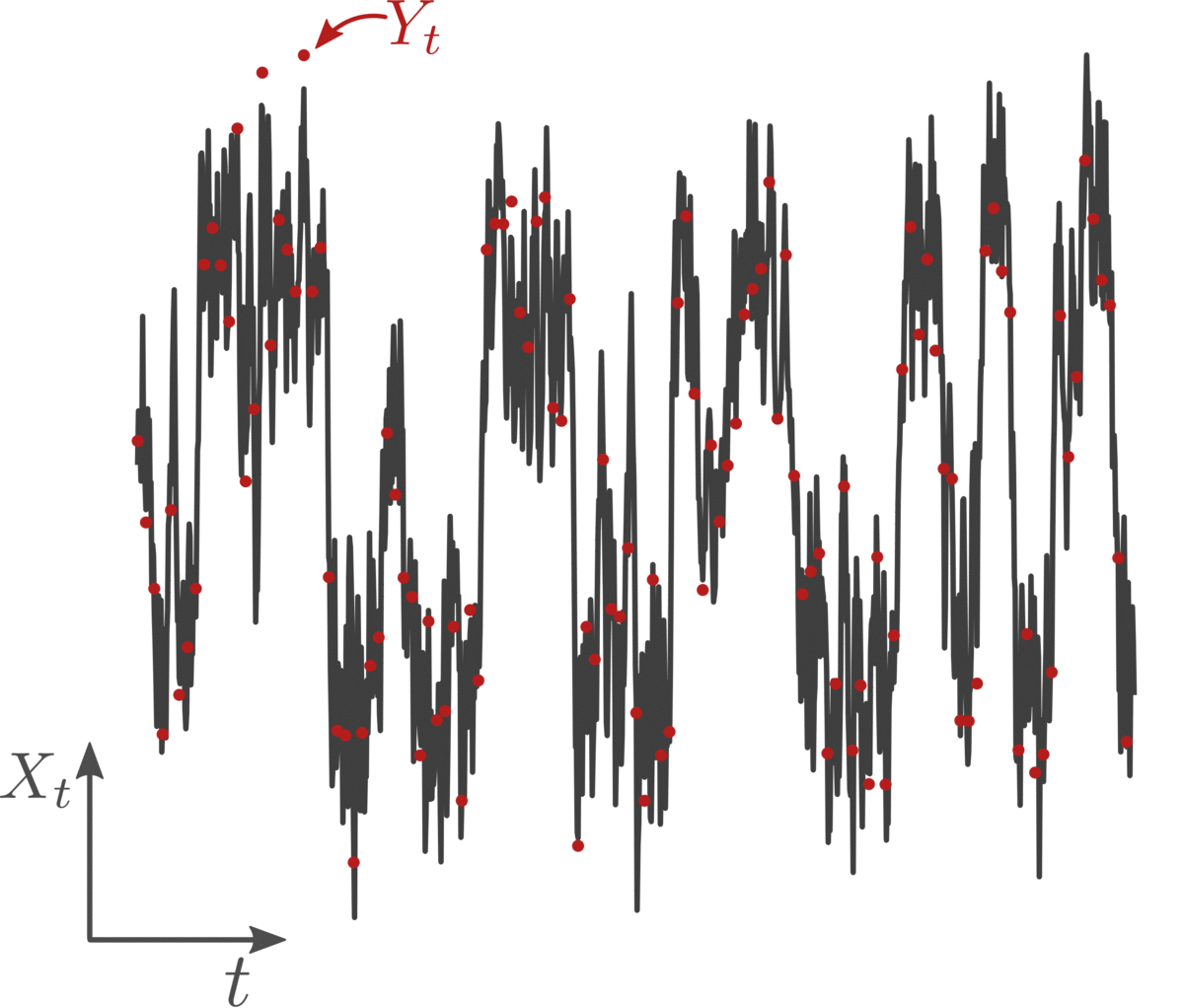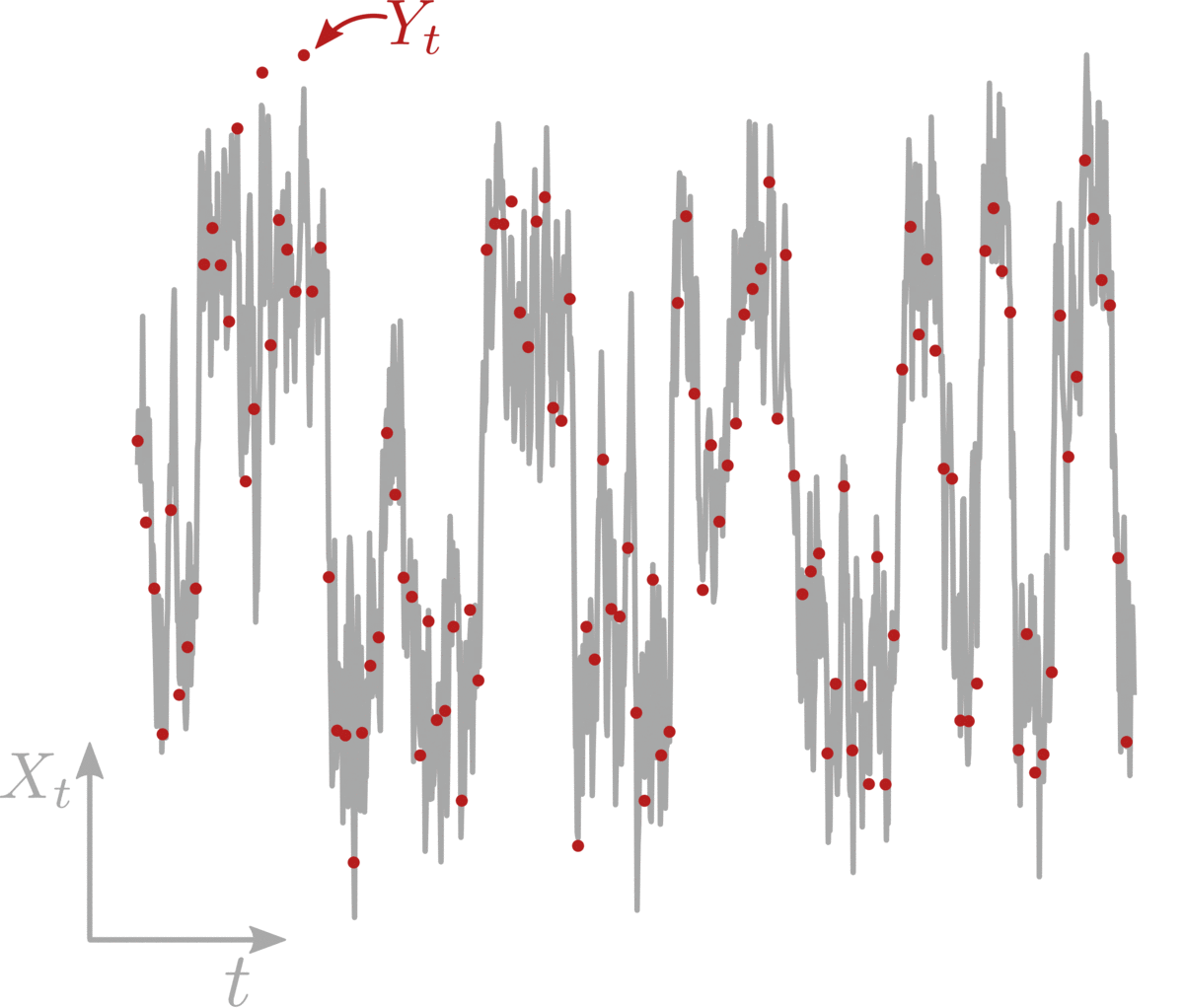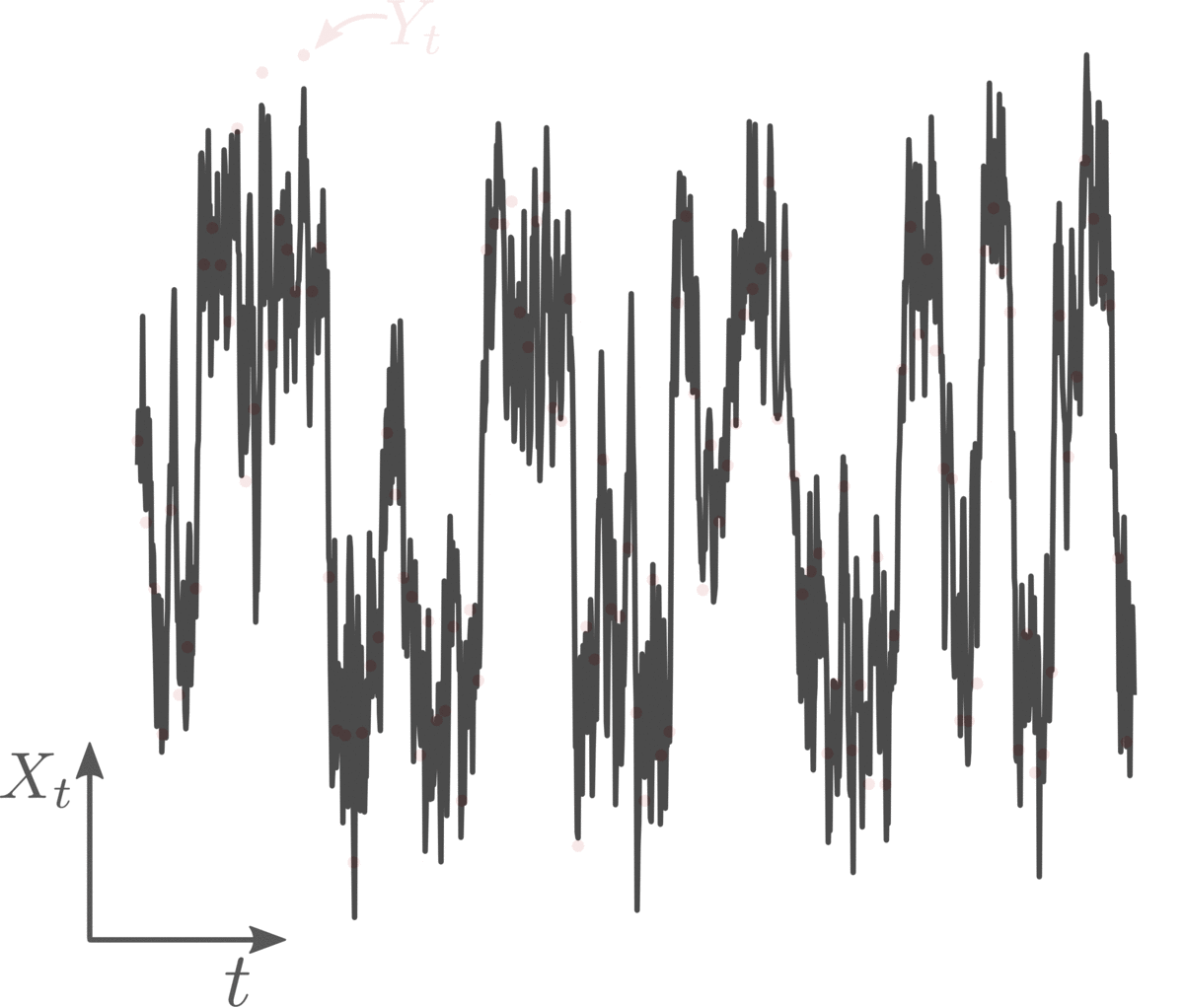
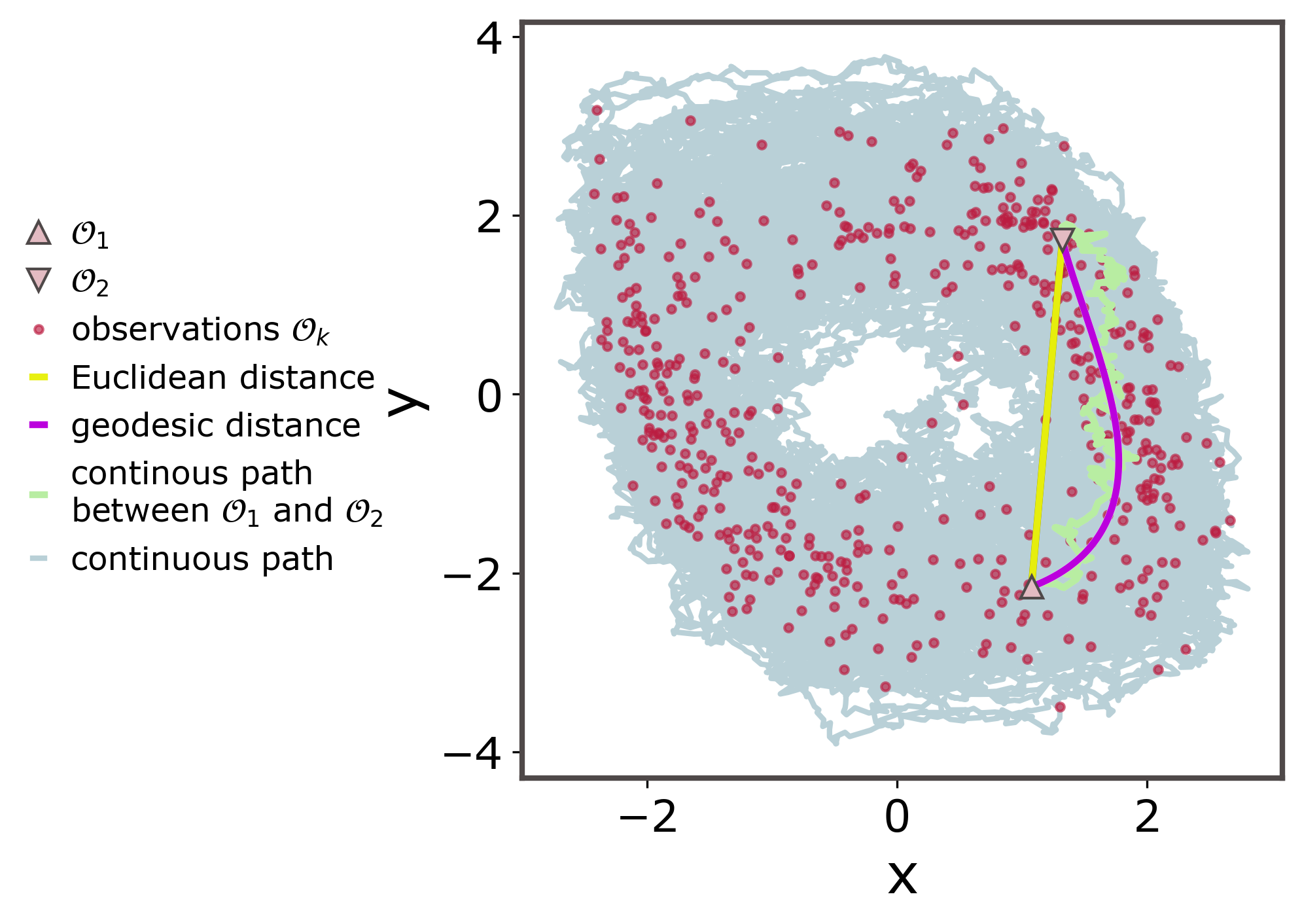
This missestimation occurs because for nonlinear systems and large inter-observation intervals the transition probabilities between successive observations strongly deviate from a Gaussian. Thus the "Gaussian" likelihood for the observations employed commonly for (nearly) continuous time measurements becomes increasingly inaccurate. We can gain further insights on the issue by adopting a geometric viewpoint. The Eucledian distances (yellow line in the figure below) employed for computing the state increments between consecutive observations in this low-frequency-observation setting do not reflect accurately the distance that we would have considered if we were observing the process in continuous time (light green line).

Existing methods for identifying the deterministic driving forces of stochastic systems rely either on approximations of the invariant density (e.g., density estimation or spectral methods like diffusion maps), or consider the temporal structure of the observations and employ path ('data') augmentation to approximate the missing paths.

However, the first ensemble of approaches is limited only to systems with conservative forces, requiring the drift to result from a gradient of a potential. On the other hand, available path augmentation methods employ simplified bridge dynamics (e.g., Brownian or Ornstein Uhlenbeck bridges) that match poorly the undelying transition density of the observed process (see next figure).

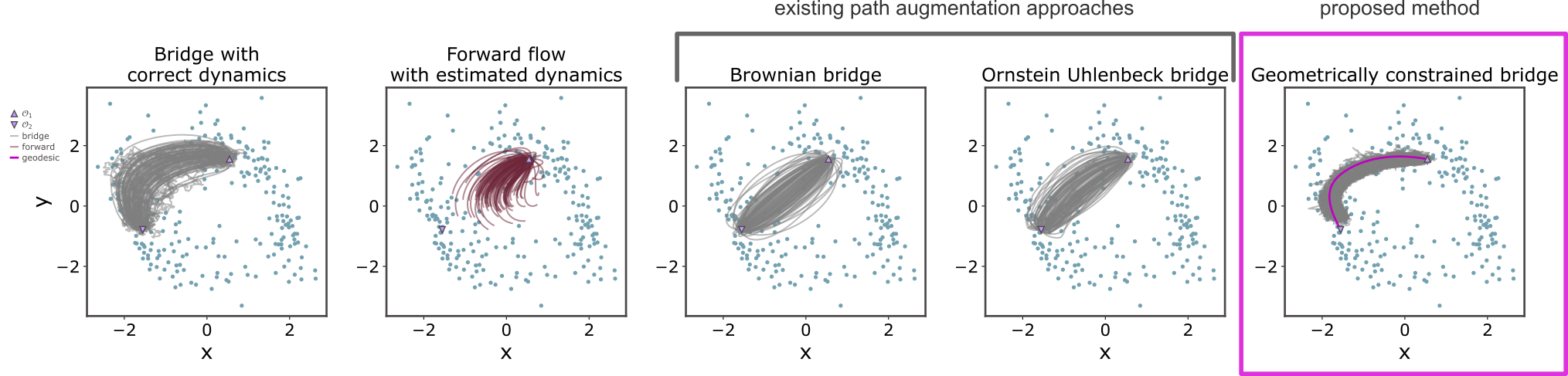
An alternative path augmentation strategy would consider a coarse drift estimate (e.g., by assuming Gaussian likelihood between observations), and would subsequently employ a stochastic bridge sampler (like the deterministic particle control framework [Maoutsa et al. 2021]) to constuct stochastic bridges with the estimated nonlinear dynamics. However, for large inter-observation intervals, the observations are often atypical states for the law of the estimated diffussion (see second plot in the figure above: starting from $\mathcal{O1}$ (upward triangle) the forward probability flow (maroon) fails to reach the second obsevration $\mathcal{O2}$ (downward triangle)). Thereby, any attempt to construct diffusion bridges with the estimated dynamics between the observations will (depending on the employed framework) either show slow convergence rates or fail completely.

Here we propose an alternative approach. We postulate that the augmented paths should lie in the vicinity of the geodesic curve that connects two consecutive observations on the empirical observation manifold. To that end we devised a path augmentation framework that constructs "controlled stochastic bridges" (formally they are not bridges any more) forcing the augmented paths towards the respective geodesics that connect two consecutive obsevrations.

But wait doesn't this contradict the Markovian property of the diffusion process? Do you construct the augmented paths by taking into account both past and future states of the process? This sounds bogus to me!

The short answer is yes and no!

We effectively construct the augmented paths to compute the likelihood of an estimated drift. However for coarse drift estimates, the observations have zero probability under the law of the estimated SDE, and approximations of the transition probability given the drift estimate are either too computationally demanding or fail altogether. Instead, here, we compute the likelihood of a "corrected" estimate (the correction resulting from the invariant density) under which the observations have non-zero probability, and subsequently re-estimate the drift on the augmented path with this "corrected" estimate.

Here we only have a coarse estimation of the drift function, and thus incorrect transition probabilities. Conditioning on the second observation in each inter-observation inteval is supposed to improve that estimate, but the transition probabilities have to be computable. By taking into account the local geometry of the observations, we provide systematic corrections for the misestimated drift function to generate the augmented paths. We effectively nudge the augmentation process towards the second observation, in the case where the construction of the diffusion bridges between consecutive observations would have been intractable otherwise.

For a Van der Pol oscillator (next figure), the initially estimated drift with Gaussian likelihood assumptions is nearly orthogonal to the ground truth force field. After only two augmentations, the estimated force field is well-aligned with the ground truth.